Drawing is an art of illusion—flat lines on a flat canvas of paper expect like something real, something total of depth. To accomplish this effect, artists employ special tricks. In this tutorial I'll show you these tricks, giving you the central to drawing three dimensional objects. And we'll do this with the help of this cute tiger salamander, as pictured by Jared Davidson on stockvault.

Why Certain Drawings Look 3D

The salamander in this photograph looks pretty iii-dimensional, right? Let's turn it into lines now.

Hm, something'southward wrong here. The lines are definitely correct (I traced them, after all!), but the drawing itself looks pretty flat. Sure, information technology lacks shading, just what if I told y'all that you can draw three-dimensionally without shading?

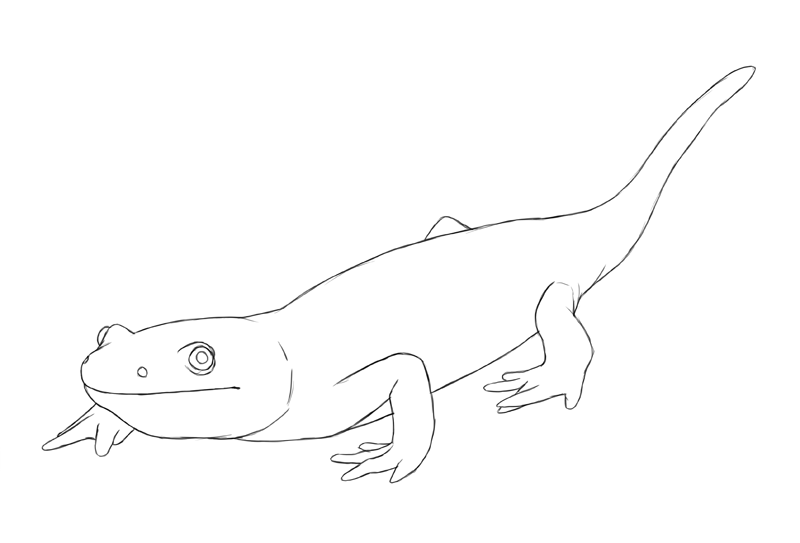
I've added a couple more than lines and… magic happened! At present it looks very much 3D, mayhap even more than than the photograph!

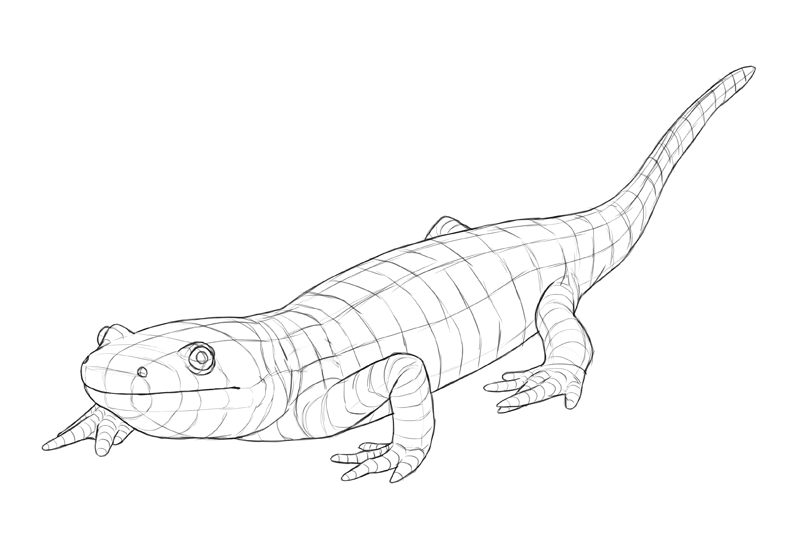
Although yous don't see these lines in a final drawing, they affect the shape of the design, skin folds, and fifty-fifty shading. They are the fundamental to recognizing the 3D shape of something. So the question is: where practise they come from and how to imagine them properly?

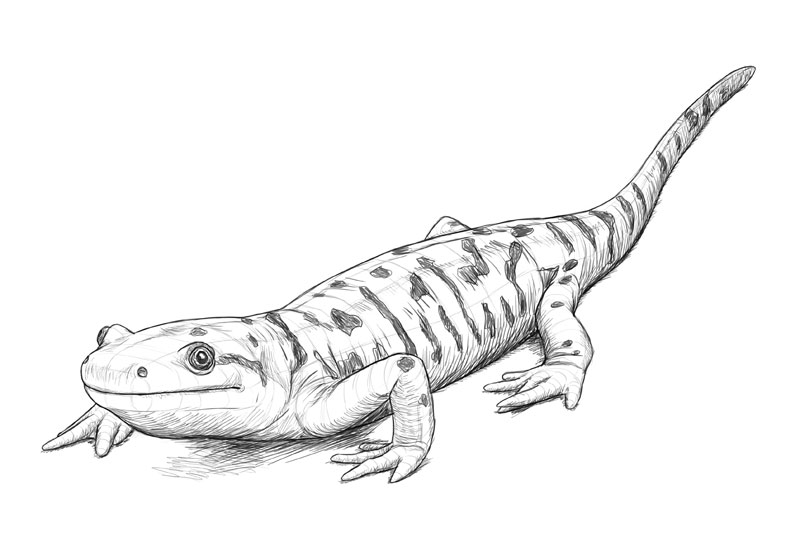
When you follow these lines with annihilation you depict on the trunk, information technology will wait as if it was wrapped around it.

3D = 3 Sides

As yous remember from schoolhouse, 3D solids have cross-sections. Because our salamander is 3D, it has cross-sections too. So these lines are nothing less, zippo more, than outlines of the body'south cross-sections. Here'south the proof:

Disclaimer: no salamander has been hurt in the process of creating this tutorial!

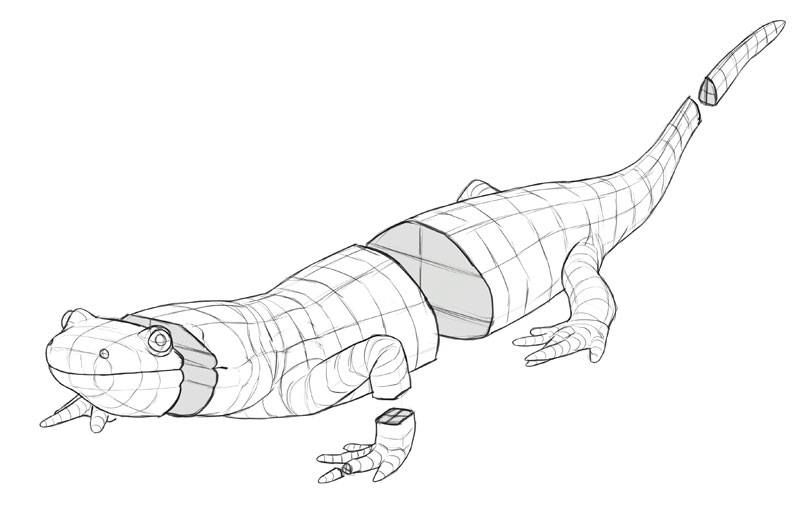
A 3D object can be "cut" in three dissimilar means, creating iii cross-sections perpendicular to each other.

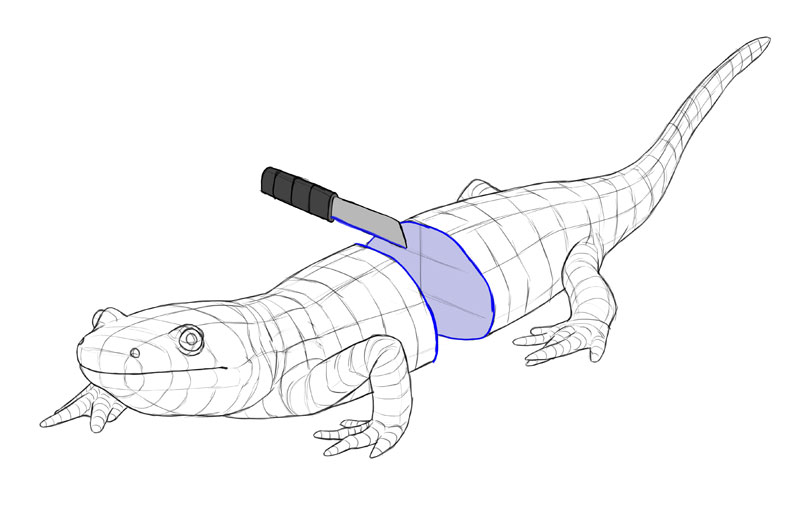
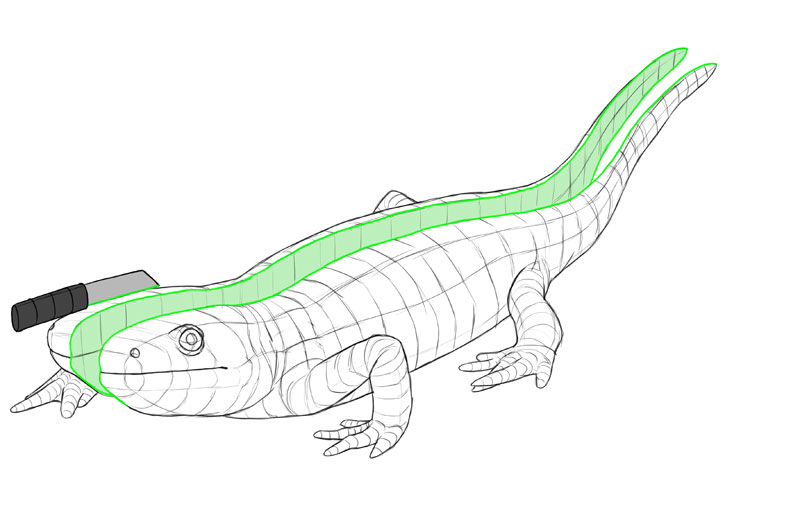
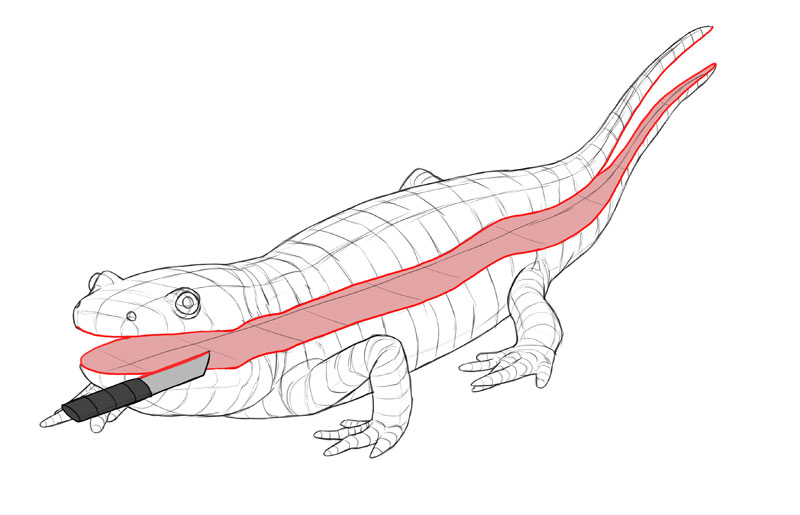
Each cross-section is 2D—which means it has ii dimensions. Each 1 of these dimensions is shared with i of the other cross-sections. In other words, 2D + 2d + 2nd = 3D!

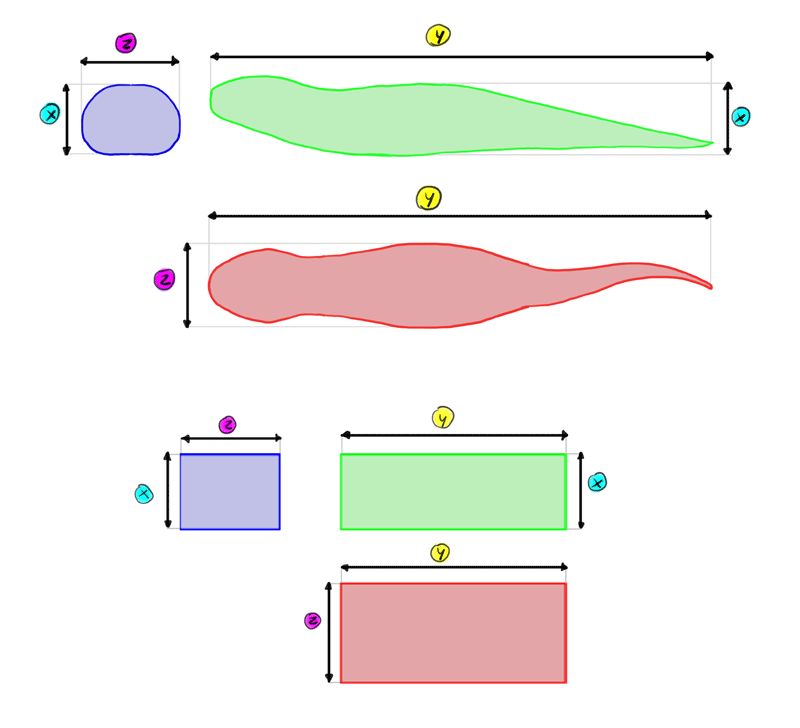
So, a 3D object has iii 2D cross-sections. These three cross-sections are basically 3 views of the object—here the green one is a side view, the blue one is the front/back view, and the reddish one is the pinnacle/bottom view.

Therefore, a drawing looks second if you tin can merely see one or two dimensions. To make information technology look 3D, y'all demand to show all three dimensions at the same time.

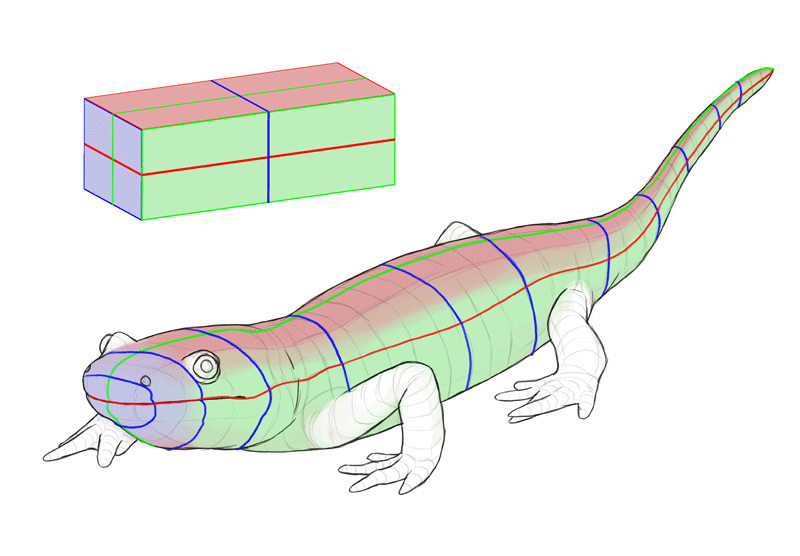
To brand it fifty-fifty simpler: an object looks 3D if you can run into at least two of its sides at the aforementioned time. Hither you tin can see the top, the side, and the front of the salamander, and thus it looks 3D.

But wait, what's going on here?

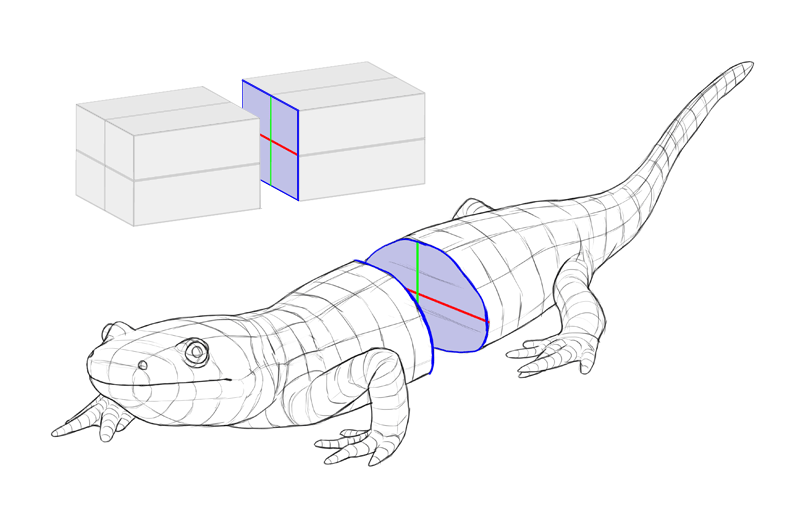
When you look at a 2nd cross-section, its dimensions are perpendicular to each other—there'south right angle betwixt them. Only when the same cross-department is seen in a 3D view, the angle changes—the dimension lines stretch the outline of the cantankerous-section.

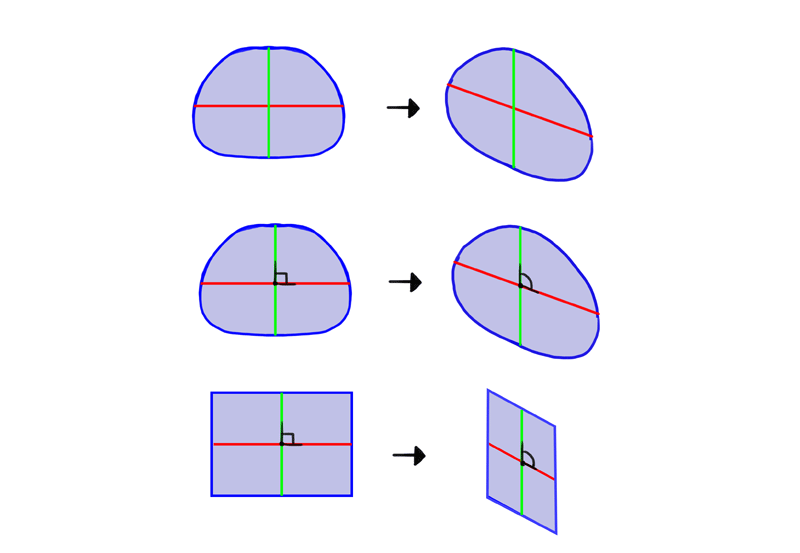
Let's do a quick epitomize. A unmarried cross-section is piece of cake to imagine, but it looks flat, because it's 2d. To brand an object look 3D, you need to testify at least 2 of its cantankerous-sections. Only when you draw two or more cross-sections at in one case, their shape changes.

This change is not random. In fact, it is exactly what your brain analyzes to empathise the view. So in that location are rules of this change that your subconscious mind already knows—and now I'thousand going to teach your conscious self what they are.

The Rules of Perspective

Hither are a couple of different views of the same salamander. I have marked the outlines of all 3 cantankerous-sections wherever they were visible. I've as well marked the top, side, and front end. Have a skillful look at them. How does each view affect the shape of the cross-sections?

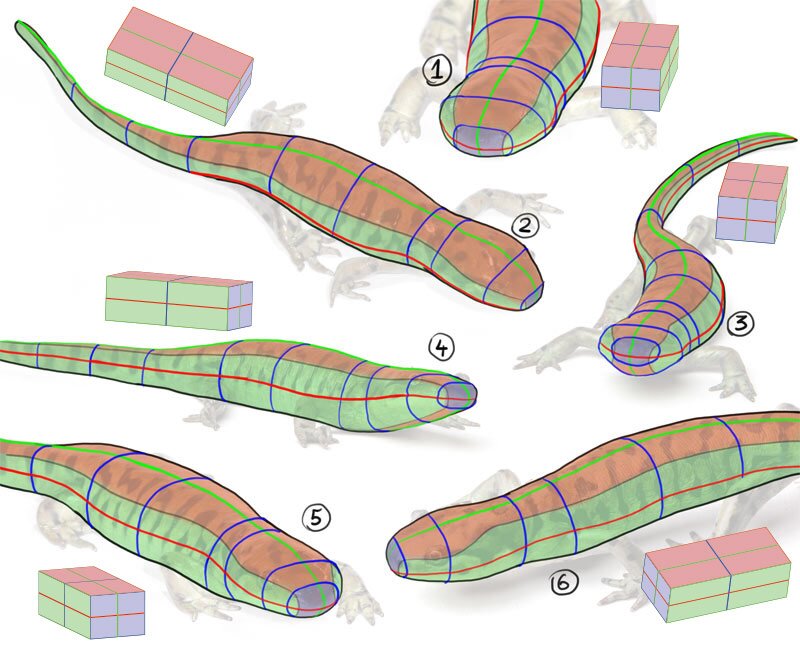
In a second view, y'all have 2 dimensions at 100% of their length, and one invisible dimension at 0% of its length. If you utilize one of the dimensions as an axis of rotation and rotate the object, the other visible dimension will give some of its length to the invisible one. If you go along rotating, one volition proceed losing, and the other will go on gaining, until finally the first ane becomes invisible (0% length) and the other reaches its full length.

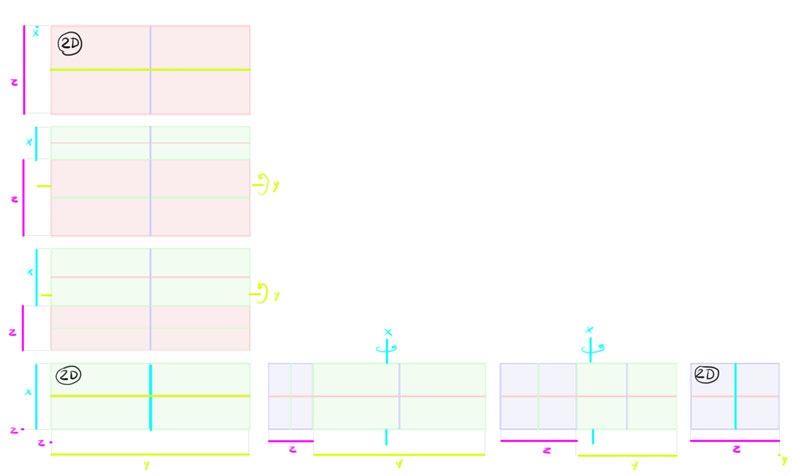
But… don't these 3D views look a little… flat? That'south right—there's one more thing that we demand to take into business relationship hither. There'due south something chosen "cone of vision"—the further you await, the wider your field of vision is.

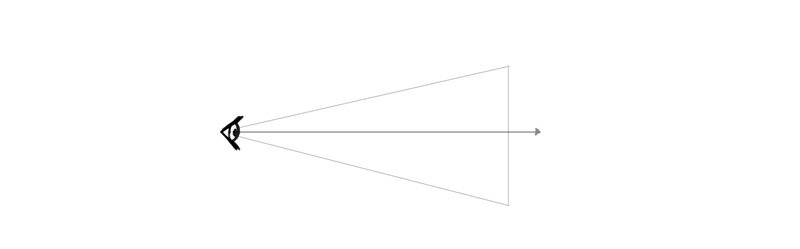
Considering of this, you can cover the whole earth with your hand if you place it right in front of your eyes, but it stops working like that when you motility it "deeper" inside the cone (further from your eyes). This also leads to a visual change of size—the farther the object is, the smaller it looks (the less of your field of vision it covers).

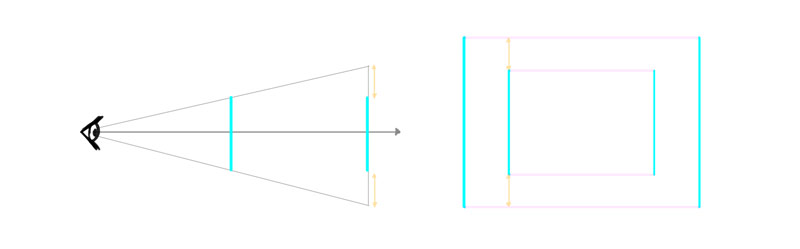
Now lets turn these two planes into ii sides of a box past connecting them with the tertiary dimension. Surprise—that tertiary dimension is no longer perpendicular to the others!

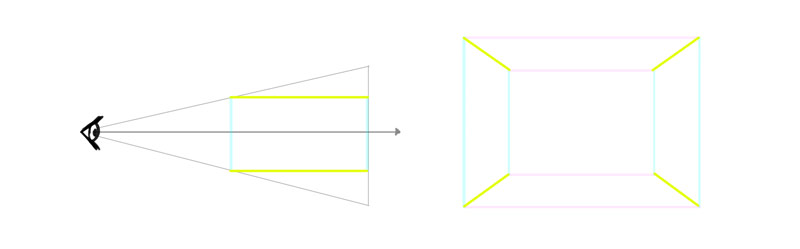
And so this is how our diagram should really look. The dimension that is the centrality of rotation changes, in the end—the border that is closer to the viewer should be longer than the others.

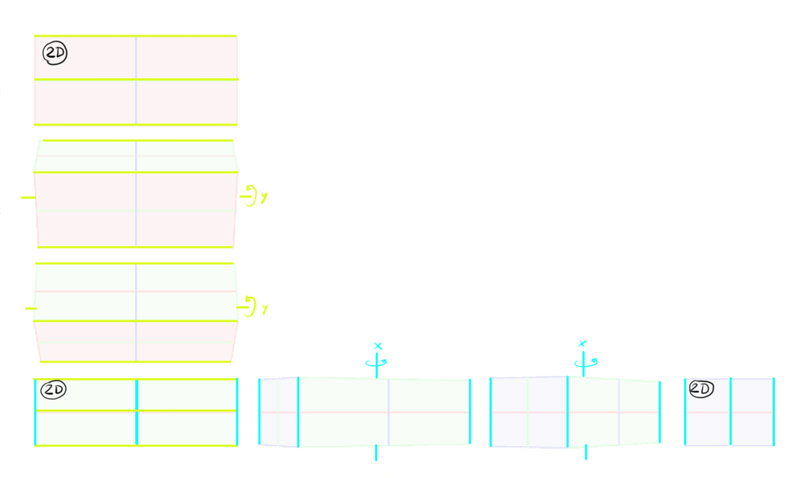
It's important to remember though that this furnishings is based on the distance betwixt both sides of the object. If both sides are pretty close to each other (relative to the viewer), this consequence may exist negligible. On the other hand, some camera lenses can exaggerate it.

So, to describe a 3D view with two sides visible, you lot place these sides together…

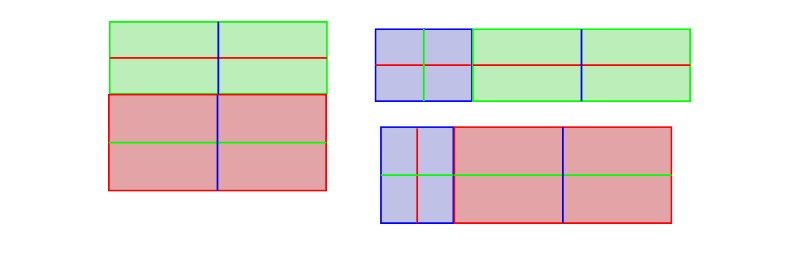
… resize them accordingly (the more of 1 you desire to show, the less of the other should be visible)…

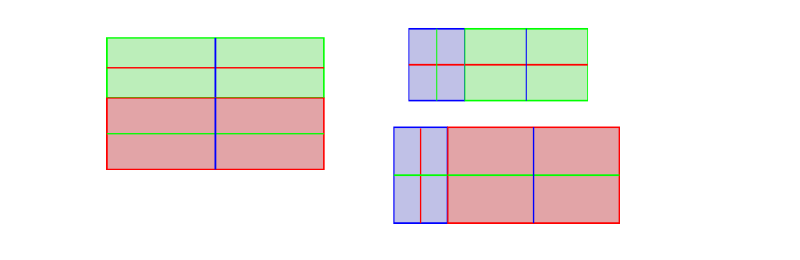
… and brand the edges that are further from the viewer than the others shorter.

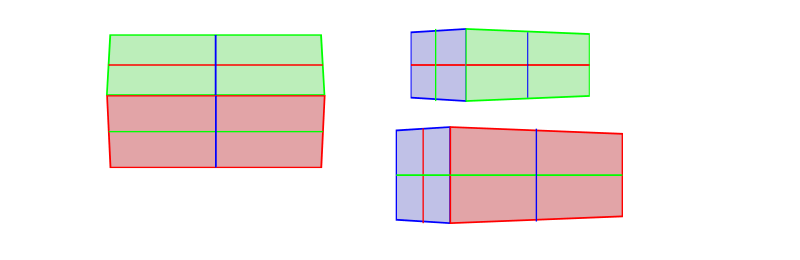
Hither's how information technology looks in exercise:

Just what about the third side? It's impossible to stick information technology to both edges of the other sides at the same time! Or is it?

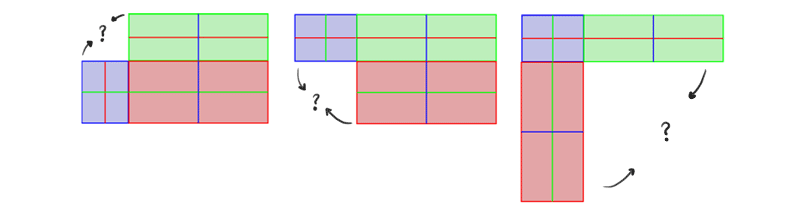
The solution is pretty straightforward: stop trying to keep all the angles correct at all costs. Slant one side, and so the other, and and then make the tertiary 1 parallel to them. Easy!

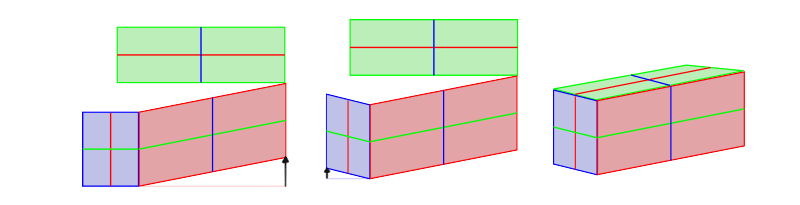
And, of course, let's not forget about making the more afar edges shorter. This isn't always necessary, but it's skillful to know how to exercise it:

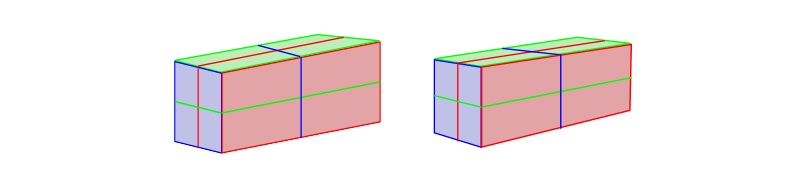
Ok, so you demand to slant the sides, but how much? This is where I could pull out a whole set of diagrams explaining this mathematically, but the truth is, I don't practise math when drawing. My formula is: the more yous slant one side, the less you slant the other. Just look at our salamanders once more and check it for yourself!

You tin also remember of information technology this style: if one side has angles shut to 90 degrees, the other must have angles far from 90 degrees

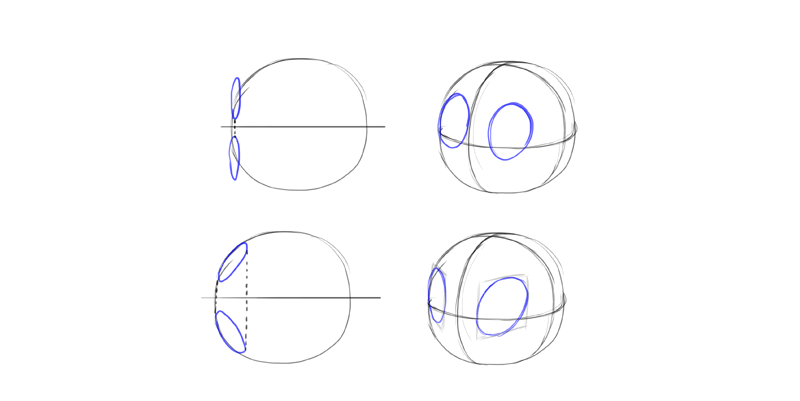
Merely if y'all want to draw creatures similar our salamander, their cross-sections don't really resemble a square. They're closer to a circle. Only like a foursquare turns into a rectangle when a second side is visible, a circle turns into an ellipse. Simply that'southward not the end of it. When the tertiary side is visible and the rectangle gets slanted, the ellipse must get slanted also!

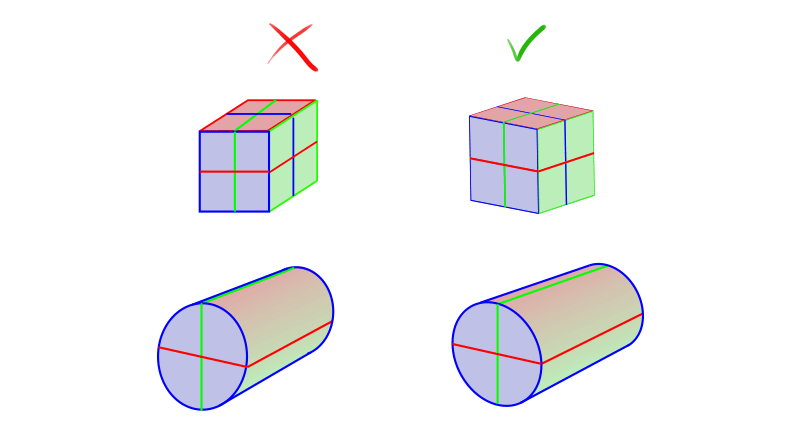
How to slant an ellipse? Merely rotate it!

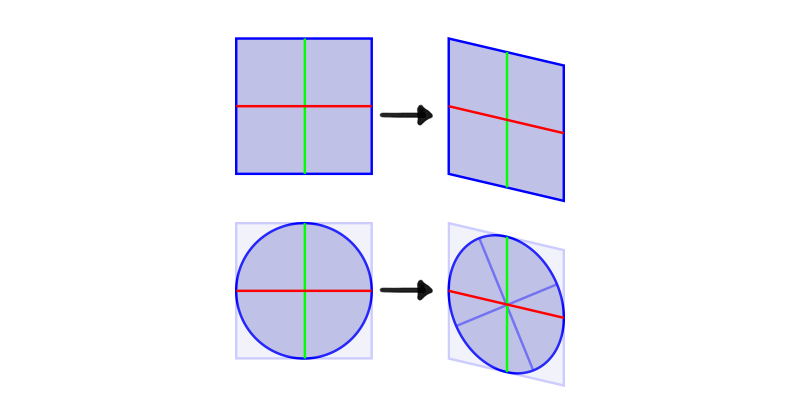
This diagram tin assistance you memorize it:

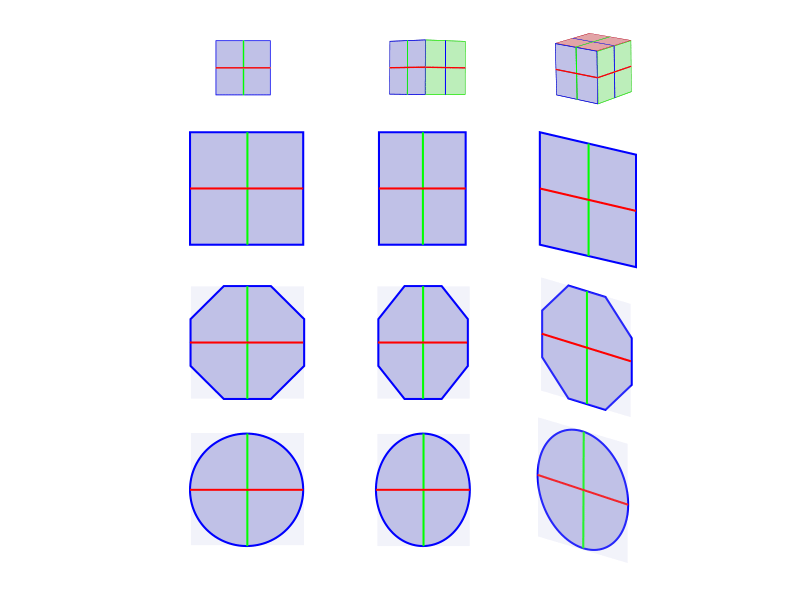
Multiple Objects

So far we've merely talked about drawing a single object. If you desire to depict two or more objects in the same scene, in that location'due south ordinarily some kind of relation between them. To show this relation properly, decide which dimension is the axis of rotation—this dimension volition stay parallel in both objects. In one case you do it, you can practice whatever you want with the other two dimensions, as long as you follow the rules explained earlier.

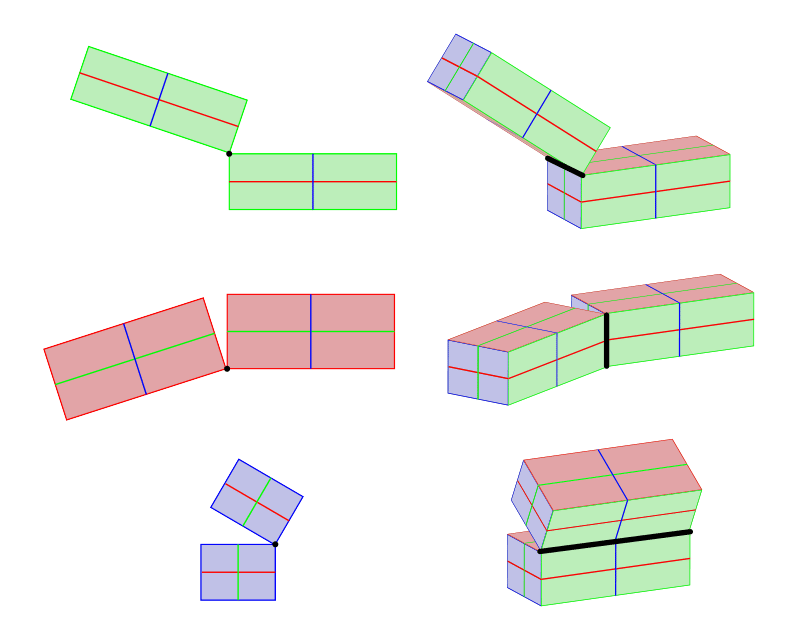
In other words, if something is parallel in one view, and then it must stay parallel in the other. This is the easiest way to check if you got your perspective correct!

At that place's another blazon of relation, called symmetry. In 2D the axis of symmetry is a line, in 3D—it's a plane. But it works simply the aforementioned!

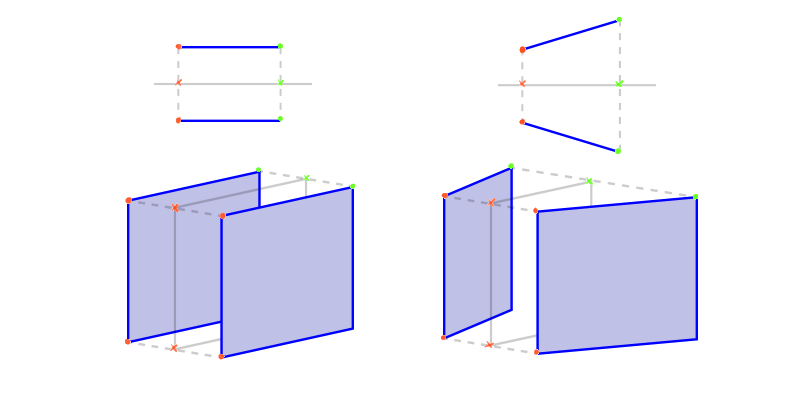
You don't need to draw the airplane of symmetry, merely you should exist able to imagine information technology right between 2 symmetrical objects.

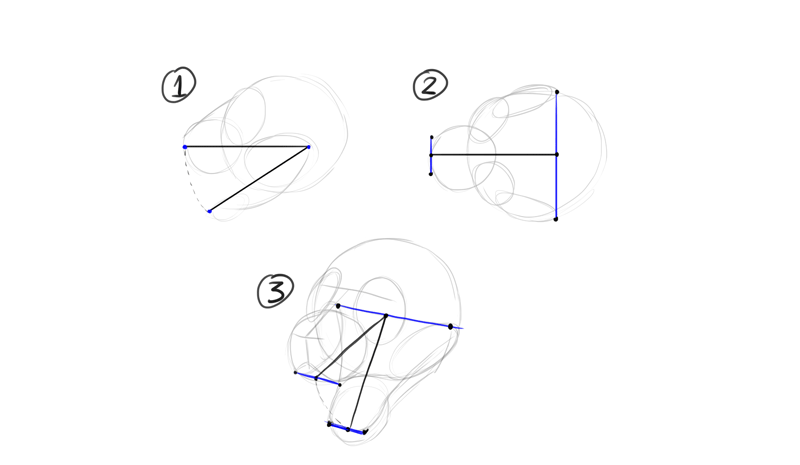
Symmetry volition aid you with difficult drawing, like a head with open jaws. Here figure 1 shows the angle of jaws, figure ii shows the axis of symmetry, and figure three combines both.

3D Drawing in Practice

Practice 1

To sympathize it all better, you tin attempt to find the cross-sections on your ain now, cartoon them on photos of real objects. Showtime, "cutting" the object horizontally and vertically into halves.

Now, find a pair of symmetrical elements in the object, and connect them with a line. This will be the 3rd dimension.

In one case you have this direction, you lot can draw it all over the object.

Go along drawing these lines, going all around the object—connecting the horizontal and vertical cross-sections. The shape of these lines should be based on the shape of the tertiary cantankerous-department.

Once you're washed with the big shapes, y'all can exercise on the smaller ones.

You'll before long detect that these lines are all y'all need to draw a 3D shape!

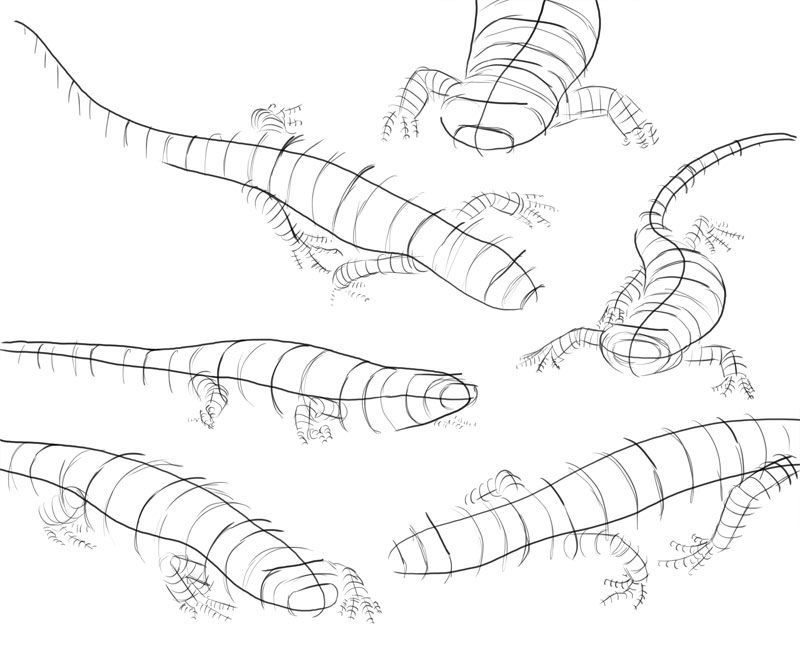
Do 2

You tin exercise a similar practice with more complex shapes, to better understand how to draw them yourself. Start, connect corresponding points from both sides of the body—everything that would be symmetrical in meridian view.

Mark the line of symmetry crossing the whole trunk.

Finally, try to find all the simple shapes that build the final class of the torso.

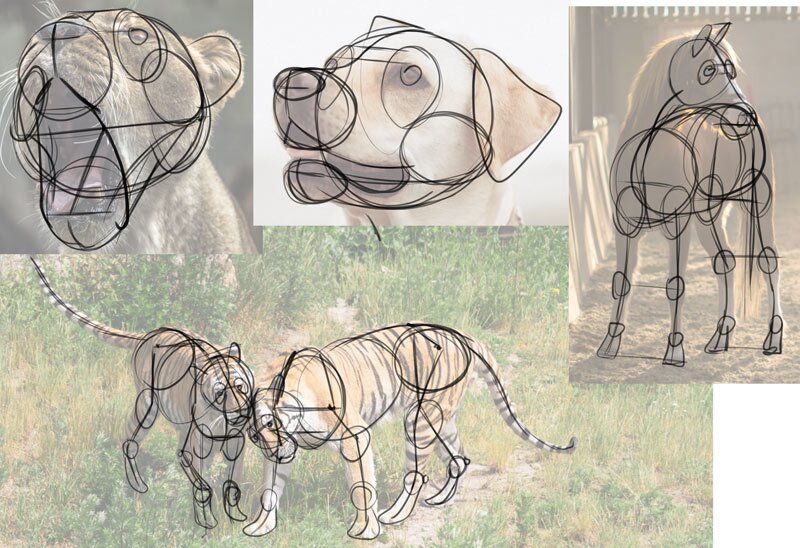
Now you have a perfect recipe for cartoon a like animal on your own, in 3D!

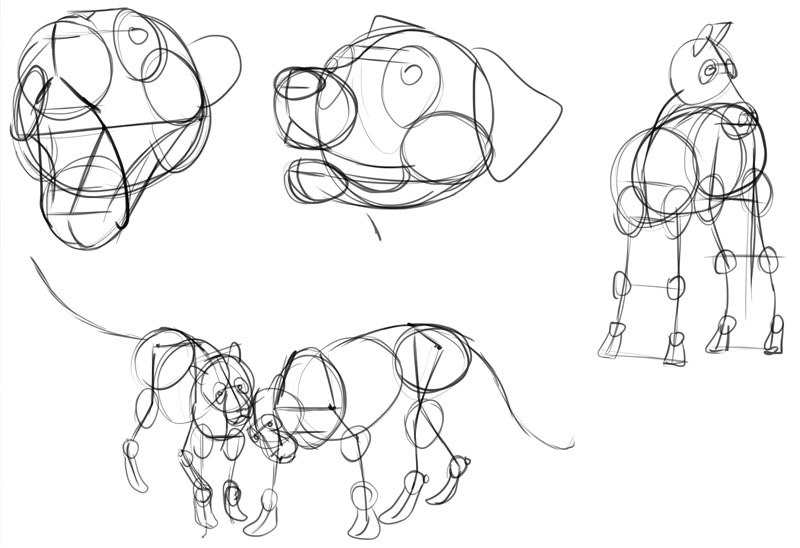
My Process

I gave you all the information you lot need to describe 3D objects from imagination. Now I'grand going to show you lot my own thinking procedure behind cartoon a 3D beast from scratch, using the knowledge I presented to you today.

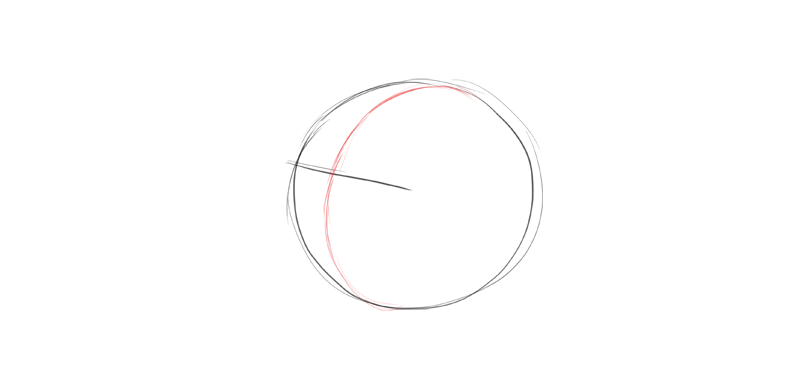
I commonly showtime drawing an animate being caput with a circle. This circle should contain the cranium and the cheeks.

Next, I describe the eye line. It'south entirely my conclusion where I want to place it and at what angle. Just one time I make this conclusion, everything else must be adapted to this offset line.

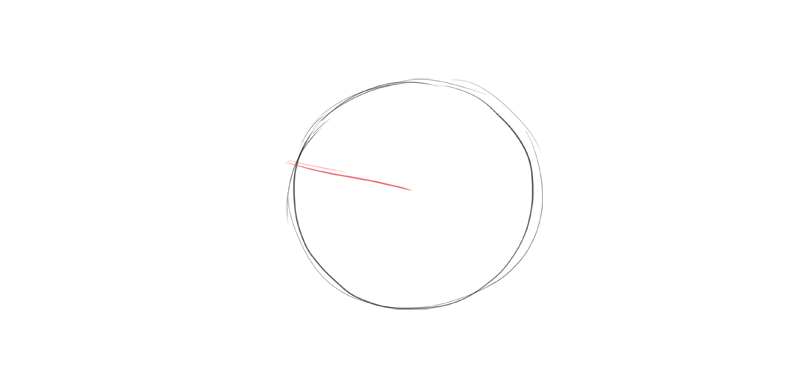
I draw the center line between the optics, to visually divide the sphere into ii sides. Tin yous notice the shape of a rotated ellipse?

I add another sphere in the front. This will exist the muzzle. I notice the proper location for information technology by drawing the nose at the same time. The imaginary airplane of symmetry should cut the nose in half. Too, notice how the nose line stays parallel to the middle line.

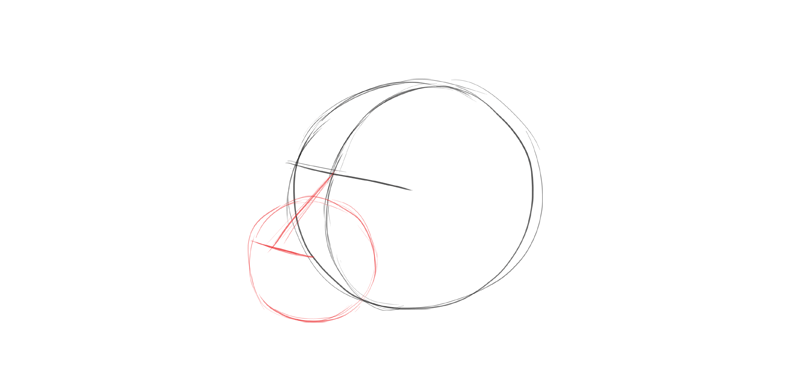
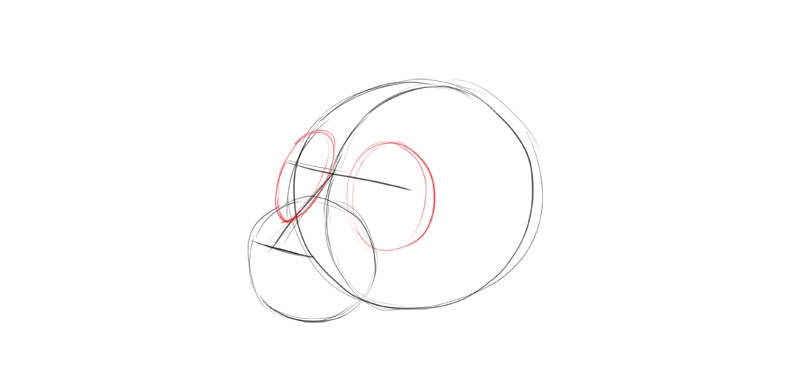
I draw the the surface area of the heart that includes all the bones creating the eye socket. Such big expanse is like shooting fish in a barrel to draw properly, and it will help me add the eyes later. Keep in listen that these aren't circles stuck to the front of the face—they follow the curve of the main sphere, and they're 3D themselves.

The oral cavity is so easy to draw at this point! I but accept to follow the direction dictated by the eye line and the nose line.

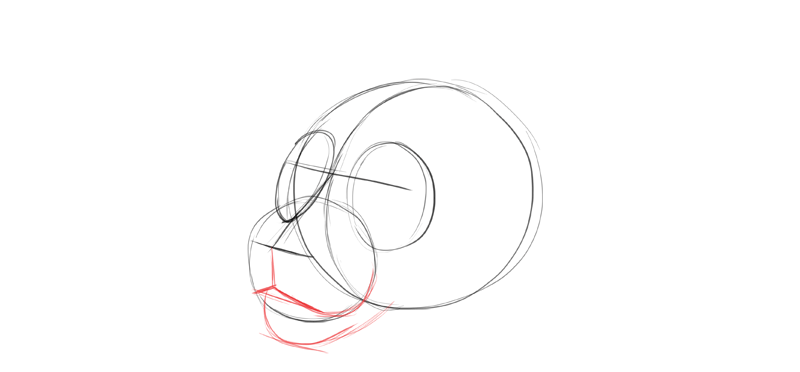
I draw the cheek and connect information technology with the chin creating the jawline. If I wanted to draw open jaws, I would draw both cheeks—the line between them would be the axis of rotation of the jaw.

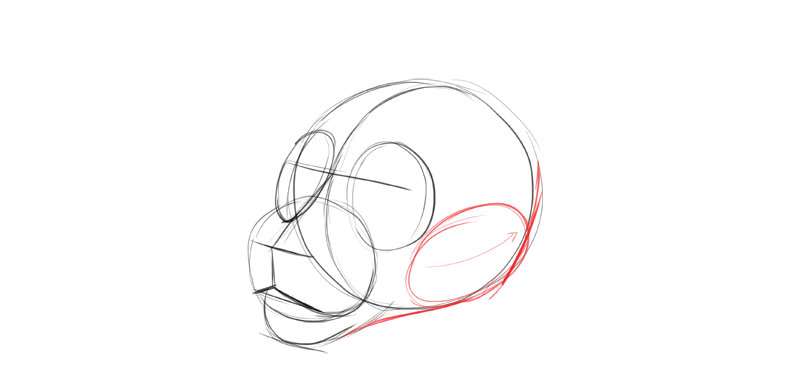
When drawing the ears, I brand sure to draw their base on the same level, a line parallel to the eye line, just the tips of the ears don't have to follow this rule then strictly—information technology's because usually they're very mobile and can rotate in various axes.

At this point, calculation the details is as easy as in a second drawing.

That's All!

It's the stop of this tutorial, only the commencement of your learning! You should now be ready to follow my How to Draw a Big Cat Head tutorial, as well equally my other fauna tutorials. To practice perspective, I recommend animals with simple shaped bodies, like:

  • Birds
  • Lizards
  • Bears

Y'all should also find it much easier to understand my tutorial most digital shading! And if yous want fifty-fifty more exercises focused direct on the topic of perspective, you'll like my older tutorial, total of both theory and practice.